题目:https://leetcode-cn.com/problems/jump-game-ii/
题目
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
说明:
假设你总是可以到达数组的最后一个位置。
解法
1. 动态规划
核心思路:先设置一个动态规划数组dp,用于暂存能够到达每一位的最短跳数。然后遍历给定数组的每一位,状态方程为 dp[i] = min(dp[i] , dp[i-k]+1)其中k为第i-k位暂存着的最短跳数。不过该方法存在一个致命的缺点,时间复杂度较高,无法通过最后一个测试点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
class Solution { public: int min(int a,int b){ if(a>b){ return b; }else{ return a; } } int jump(vector<int>& nums) { int len = nums.size(); int dp[len+1] ; for(int i=0;i<len+1;i++){ dp[i]=999999; } dp[1] = 0; for(int i=1;i<=len;i++){ for(int j=i+1;j<=(i+nums[i-1]);j++){ if(j>len){ break; } dp[j] = min(dp[j],dp[i]+1); } } return dp[len]; } }; |
2. 贪心算法
LeetCode 讨论里,大部分都是这个思路,贪婪算法,我们每次在可跳范围内选择可以使得跳的更远的位置。
如下图,开始的位置是 2,可跳的范围是橙色的。然后因为 3 可以跳的更远,所以跳到 3 的位置。
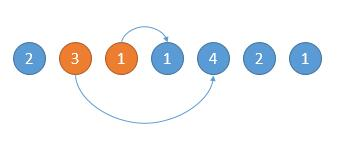
如下图,然后现在的位置就是 3 了,能跳的范围是橙色的,然后因为 4 可以跳的更远,所以下次跳到 4 的位置。
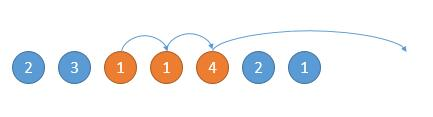
写代码的话,我们用 end 表示当前能跳的边界,对于上边第一个图的橙色 1,第二个图中就是橙色的 4,遍历数组的时候,到了边界,我们就重新更新新的边界。
总而言之,由于题目规定,可以在范围内任意步数跳跃,因此可以采用了尽可能长的贪婪思想,eg,当nums[0] = 2时,在nums[1],nums[2]中选择拥有最长的,这样,最长的自动把最短的包括进去了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
class Solution { public: int jump(vector<int>& nums) { int maxpos=nums[0]; //最远能够跳的距离 int curpos=0; //当前边界检测距离 int step=0; for(int i=1;i<nums.size();++i){ if(i>curpos){ //如果当前扫描的点超过了边界 curpos=maxpos; //边界赋予新的最远距离 step++; } maxpos = max(maxpos,nums[i]+i); //计算最远距离 } return step; } }; |
